Brief Notes On Int8 Quantization And Inference Developments

03/2023 - Phil

Mainly summarizing how LLM.int8() works and some remarks on doing more with less.

Problem:

• Models have gotten really large. A 20B parameter model on fp32 is 80GBs.
• An A100 is 80GBs of memory. Most commercial GPUs have far less VRAM and host memory to store these models.
• These large models hog a ton of memory.
• Note while latency is nice and we might get latency improvements, the main consideration with quantization here is memory usage and not stepwise latency.

Remedy:

• Find some clever way of using a smaller datatype. If we could use 8 bits instead of 32 bits we could shrink memory usage up to 4x.

Considerations:

• We want to shrink the model down to smaller datatypes while not degrading performance too much.

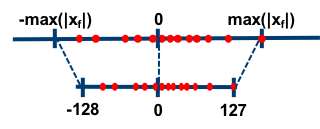
Absmax Quantization

Consider a matrix \(\mathbf{X}_{f16}\in\mathbb{R}^{s\times h}, \mathbf{W}_{f16}\in\mathbb{h\times o}\) (in fp16). Then $$\frac{\mathbf{X_{f16}}}{

\mathbf{X}_{f16}

_\infty}\(has range\)[-1,1]\((note that\)

\cdot

_\infty=\max{

X_{ij}

:i\in{0,1,\ldots, s-1}, j\in{0,1,\ldots,h-1}}$$). So

\[\mathbf{X}_{i8}=\text{round}(127\frac{\mathbf{X_{f16}}}{||\mathbf{X}_{f16}||_\infty})\]

has range \([-127, 127].\) Therefore we can approximate \(\mathbf{X}_{f16}\approx \frac{\mathbf{X}_{i8}}{s_{xf16}}.\)

Now we want to be able to perform matmul with int8:

\[\begin{align*} \mathbf{X_{f16}}\mathbf{W_{f16}}&\approx \frac{\mathbf{X_{i8}\mathbf{W_{i8}}}}{s_{xf16}{s_{wf16}}}\\ &=\frac{\mathbf{C_{i32}}}{s_{xf16}{s_{wf16}}}. \end{align*}\]

This means we convert our fp16 matrices to int8, multiply them, then divide by fp16.

Absmax quantization

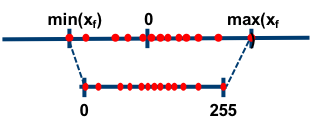
Zeropoint Quantization

This is similar to Absmax but now instead of mapping to \([-127, 127]\) we map to \([0, 255]\) by shifting our values so that that our minimum value starts at zero. By doing this we use the full range of values from \([0, 255].\) With absmax quantization we are simply rescailing, and if, say, most of our values are positive we won’t be using much from \([-127, 0),\) leading to more quantization error.

Zero point quantization is as follows:

\[\begin{align*} nd_{x16}&=\frac{255}{\max\mathbf{X_{f16}}-\min\mathbf{X_{f16}}}\\ zp_{xi16}&=\text{round}[\mathbf{X_{f16}}\min\mathbf{X_{f16}}]\\ \mathbf{X_{i8}}&=\text{round}[nd_x\mathbf{X_{f16}}],\\ \mathbf{C_{i32}}&=(\mathbf{X_{i8}}+zp_{xi16})(\mathbf{W_{i8}}+zp_{wi16})\\ \mathbf{X_{f16}}\mathbf{W_{f16}}&\approx\frac{\mathbf{C_{i32}}}{nd_{x16}nd_{w16}}. \end{align*}\]

Note that our GPU needs to be able to accumulate multiplication into int16 int int32 for \(C_{i32},\) otherwise we need to expand and multiply each term separately.

Zero point quantization

Dealing with outliers

When we have a massive matrix \(\mathbf{X_{f16}}\) scailing by the min or max is going to destroy a lot of information due to outliers. The basic remedy here is to selectively apply our quantization to different parts of the matrix.

One straight forward way is to quantize the rows of \(\mathbf{X_{f16}}\) and the columns of \(\mathbf{W_{f16}}\) separately. Then we end up with vectors \(\mathbf{c_{xf16}}\in\mathbb{R}^s, \mathbf{c_{wf16}}\in\mathbf{R}^o,\) which hold the scailing factors. Then after computing these vectors our quantized multiplication becomes \(\mathbf{X_{f16}}\mathbf{W_{f16}}\approx\frac{1}{\mathbf{c_{xf16}}\otimes\mathbf{c_{wf16}}}\cdot\mathbf{C_{i32}}\) where \(\otimes\) is the outer product.

Doing this is going to be a lot better than naive zeropoint or absmax quantization. However, there’s still large performance degradation.

There are a few things that are good to know about the outliers in the model:

• Most rows for \(\mathbf{X_{f16}}\) (typically the context window) have outliers, so quantizing these rows are still going to have lots of error.
• Most columns of \(\mathbf{X_{f16}}\) don’t have outliers. The outliers are systmatically concentrated. In the Dettmers paper, a 13B parameter model has no more than 7 columns containing the outliers.
• Removing the 7 outlier feature dimensions results in perplexity increase of 600-1000% whereas removing 7 random feature dimensions results in negligible performance change.
• Outlier magnitudes get larger as the number of parameters grow.
• Percentage of layers affected by an outlier increases monotonically, with a large increase after around 7B parameters. These outliers also increasingly affect the same dimensions across layers.

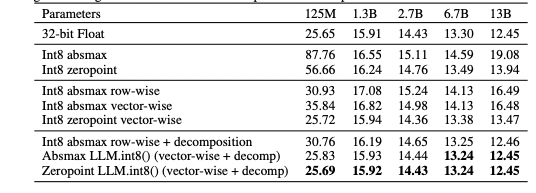
Using these facts one remedy is to use mixed-precision decomposition. As most of the outliers are in a small number of columns of \(\mathbf{X_{f16}}\), we can separate those columns out and multiply them separately with the outlier rows of \(W_{f16}\) using normal fp16 matmul and multiply the rest using our quantization methods. After decomposing, we can merge the decomposed matrices back into our output matrix. Since the dimensions affected are not larger than 7 for a 13B parameter model, 99.9% of our values are 8-bit.

Using this decomposition method the Dettmers paper is able to achieve 32bit float perplexity on int8:

LLM.int8()

If your model is in PyTorch (and you have a CUDA GPU), one can probably use the bitsandbytes wrapper pretty straightforwardly. It’s as simple as replacing torch.nn.Linear(...) with bnb.nn.Linear8bitLt(...) with threshold=k set.

A lot of people might be CPU memory bound still as we still need to load the original model into DRAM, so one can create a swapfile to offload any extra memory into disk. I’m guessing one could skip some of this CPU memory usage in the future if they already precomputed the conversion and prestored the int8 and scaling factors too.

Note that huggingface also already integrates with bitsandbytes pretty conveniently.

Implementation of INT4

We can use even fewer bits if we want. Empirically it seems that going down to int4 does not damage performance much, although we start seeing more degradation once we use int3. I would not be surprised if many commercial models are using int4 quantization.

Currently LLM.int8() does not support int4 quantization although it might soon. I am planning on working to rush out a naive form of int4 (potentially slow kernel but saves on memory).

There are a few reasons why GPU int4 isn’t as widely available to developers currently (although I suspect it might be soon):

• On the PyTorch level, tensors only support down to int8 or bool.
• CuBLAS does not default have int4 operations. Therefore we may need to move in the kernel level to support this.

There isn’t theoretically anything about int4 that makes it that much harder than int8. There are just slightly more implementation details as fewer people are comfortable working on the kernel level and the NVIDIA documentation isn’t super transparent.

Basic plan of attack:

• WMMA provided by NVIDIA allows us to do int4 tensor operations. This is a warp level operation and it seems we need to pass in matrices of size 8x4 int32 to use it. The 4 ints column wise are interpreted as 8 int4s. Then we need to incorporate the warp level operation into an actual GEMM kernel to be able to multiply matrices.
  • I’m not an expert here but if we were to write a CPU version, to do it fast we’d want to be able to take advantage of SIMD operations (single instruction multiple data) which will allow the CPU to do some parallelization. How one does this will depend on the CPU architecture. We can probably also do an easier naive version that runs slower without as many considerations.
• To store the int4 values in PyTorch we pack the values in the way the int4 WMMA wants us to–we pack values in an int32 tensor by bitshifting values together.
• Stack trace is something like: LinearInt4Module().forward(x) -> quantize and pack values (if not stored before) -> lookup custom int4 kernel -> dequantize kernel output and return fp16 output.

Remarks on some developments

• Using quantization one can use more powerful models on cheaper hardware. For example LLaMa-13B on fp16 is going to be 26GBs, but an RTX 4090 (around $2000) is only 24GB of VRAM. With LLM.int8() one can make minor modifications to the code and now the entire model can fit into VRAM.
• The FlexGen demonstrates that if one is not as worried about latency, one can run a KV cached 175B parameter model on a single 16GB NVIDIA T4 (around $2000). A single layer of GPT-3 175B (96 layers) can fit on 16GB. So if we are okay paying the memory transfer costs of loading on and off VRAM (onto DRAM) for each layer, by converting to 4 bit datatype we can actually use a pretty large batch size on a single cheap GPU. Note that this isn’t necessarily the most practical strategy because while we can achieve high throughput with a large batch size we are still taking a really long time per step. So unless we have some user case where the user is fine waiting more than a minute per token, this isn’t really that useful as it might seem on the surface.
• The Chinchilla paper makes some interesting analyses on scailing for LLMs. The basic takeaway is in addition to scaling with parameter size, we can improve LLMs by also training on more tokens. Basically we can achieve better performance by training a smaller model for longer on more tokens. This is corroborated by LLaMA where a 7B parameter model achieves similar benchmark scores as GPT-3 175B.
• One should note that better performance on benchmarks like common sense reasoning do not necessarily mean better performance in real life. One should also note that ChatGPT is not a vanilla language model but one that has been finetuned with RLHF, so one should not expect LLaMA or FLAN models to generate similar responses. It is also certainly a possibility that the real resource intensive thing for “ChatGPT use” is the ability to do RLHF, and that without this the models are not as interesting aside from performing well on benchmarks. It also seems true that optimizing large scale training with less resources is a much harder problem than optimizing inference.
• There is an interesting direction that I can see playing out, however. There may be a future where it is increasingly easier to use very good LLMs requiring less expensive hardware and that there will be an open source culture of modifying models like LLaMA for practical use locally. It would also be cool if people figure out how to do low cost RLHF (although I could see where this is infeasible). Imagine crafy individuals being able to run a DaVinci quality model on their own GPU and being able to tune it to various bespoke needs and then releasing such models to the public.