Power Law Scaling And Zipf's Law

03/2025 - Phil

The ostensibly magical properties ascribed to the mere scaling of artificial intelligence models warrants closer examination. Upon consideration, it becomes evident that the distinctly mathematical relationship between resources and performance improvements may be fundamentally connected to the underlying statistical structure of language itself.

It is my contention that the power-law scaling observed in large language models–noted by the DeepMind Chinchilla paper–stands in direct relation with Zipf’s law or some other statistical artifact of language¹. The commonly cited scaling law is that a large language model’s loss function as a function of model size \(N\) and training steps \(D\) is \(\hat{L}(N,D)=E+\frac{A}{N^\alpha}+\frac{B}{D^\alpha},\) where \(E\) is a constant.

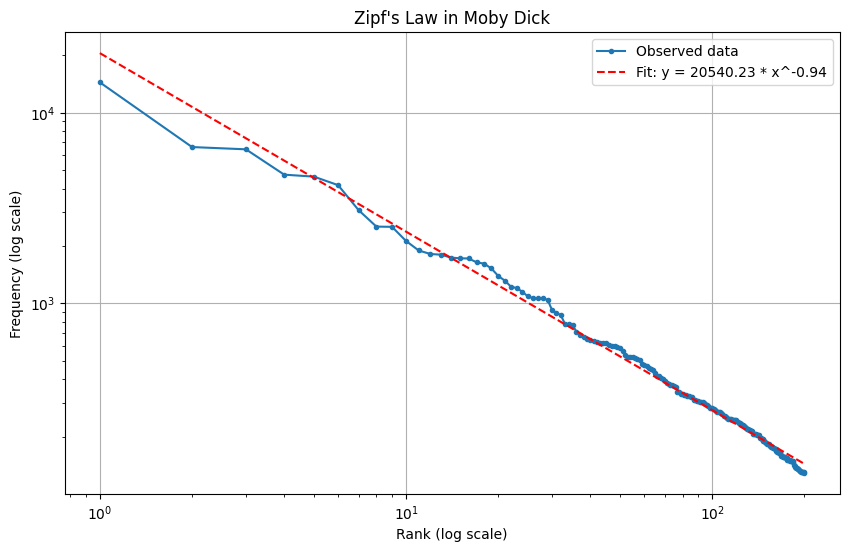
Zipf’s law, when applied to practically any text, demonstrates with remarkable consistency that the frequency of any word is inversely proportional to its rank in the frequency distribution–the \(n^\text{th}\) most common word occurs with a frequency proportional to \(1/n\). This distribution extends well beyond language, manifesting in income distributions, population densities of urban centers, and numerous other natural and social phenomena. The Pareto principle—which stipulates that approximately 80% of consequences stem from 20% of causes—emerges as a natural corollary to Zipf’s law, both being manifestations of the same underlying power-law distribution that governs these fundamental imbalances. If one were to encounter a low frequency word that occurred \(0.001\)% of the time in a sentence, sampling at random it would take in expectation one hundred thousand words to encounter that word again. Contrast that with the word “the” which one would expect to encounter every 20 words. It is possible that this dramatic non-linearity may be related to the curve of a loss function.

Pick a arbitrary text in Project Gutenberg and it will follow Zipf’s law.

Shannon’s foundational work on information theory provides a framework for understanding these relationships². He defined redundancy as one minus the relative entropy ratio–the ratio between the entropy of the language and the maximum possible entropy for that character set. In a language devoid of redundancy with maximum compression—one that approaches maximum entropy—each symbol would occur with equal probability, nullifying Zipf’s law³.

Shannon defines information content of an event \(x\) as \(I(x) = -\log P(x)\). This formulation implies that rarer terms such as “Etruscan” or “oligarchy” convey greater information than common terms like “he” or “year.”

Let us consider, for analytical purposes, a simplified model wherein human language comprises discrete, disjoint units of knowledge—distinct “concepts” that follow a Zipfian distribution. Under such conditions, what relationship emerges between the quantity of data processed and the cumulative knowledge acquired?

If there are \(N\) distinct concepts, Zipf’s law says the probability of the \(n^\text{th}\) item is \(p_n=\frac{k}{n}.\) If we have observed \(t\) examples, the probability that item \(n\) has not been seen is \((1-p_n)^t.\) So the probability that item \(n\) has been seen at least once is \(1-(1-p_n)^t.\) In this case, the contribution to total knowledge will be equal to \(\log\frac{n}{k}.\) The expected value of total knowledge at time \(t\) is then \(f(t)=\sum_{n=1}^N[1-(1-p_n)^t]\log\frac{n}{k}.\) What we have here is not a power-law per se, but an exponential convergence towards total knowledge capacity.

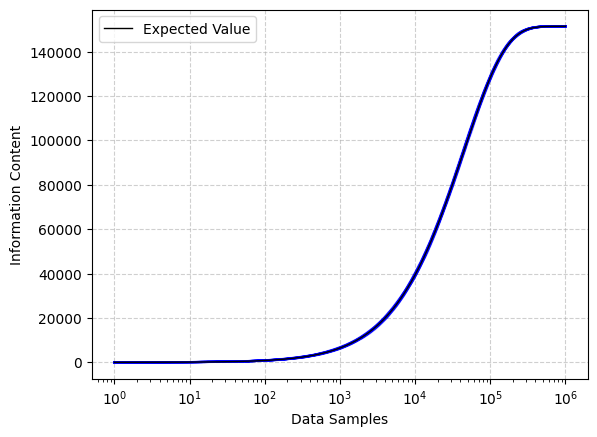
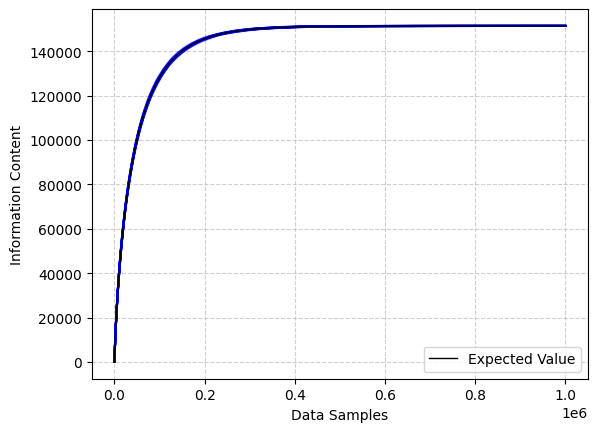
I confirmed this expected value through one hundred computational simulations with ten thousand distinct concepts observed across one million randomly sampled examples reveals a pattern. Assuming perfect learning efficiency, where a concept, once encountered, is perfectly learned, we observe an uncanny pattern of knowledge acquisition–appearing similar to a LLM loss function. Note that the cross-entropy loss is a measure of difference in information content between two different distributions–a decrease in the loss function means a smaller difference in information content between the actual distribution and the language model.

Blue lines indicate a tight adherence of simulation paths to expected value. A brief period of rapid learning followed by an asymptote towards capacity.

The simulations demonstrate an initial period of rapid learning, during which commonly occurring concepts are quickly assimilated, followed by a prolonged phase of diminishing returns as the model occasionally encounters increasingly rare concepts. This pattern emerges specifically when observations are sampled in an independent, identically distributed manner. Note that if our items were uniformly distributed as opposed to Zipfian we would observe learning that approached the asymptote much faster.

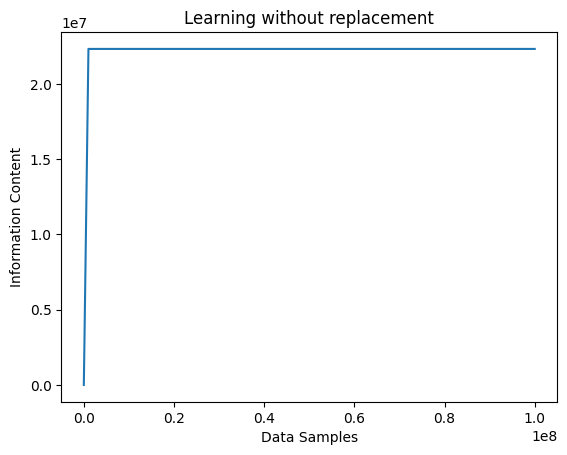
If, however, one were to employ a more efficient sampling strategy—targeting only previously unobserved concepts—this relationship disappears, replaced by a linear learning curve that reaches total knowledge capacity in a substantially shorter period of time.

Sampling without replacement, the model acquires all knowledge faster.

These toy simulations suggest that the scaling observed in loss functions may derive from a redundancy encountered through random sampling. To my understanding, the Chinchilla power-law scaling is primarily based on empirical observation of the loss functions of LLMs as one adjust parameters and data size rather than theory, but perhaps there is a bottom-up framework that might explain these trends. I’d be interested in further exploring ways we can use information theory to fit the empirical loss curves.

Once confronting the “data wall”—the point at which we run out of novel internet text—it seems possible that one can continue meaningful improvements to artificial intelligence by creating high-information content data from distributions on which the model performs poorly. For example, through a combination of manual curation and reinforcement learning set-ups one could induce additional high quality samples in mathematical reasoning. This synthetic data, if high enough quality, could potentially lead to steeper model improvement rate than typical power-law scaling. The recent rapid improvement in model ability to solve difficult math olympiad questions appears more a consequence of this approach than merely increasing the magnitude of the general dataset.

One might question, reasonably so, whether there are immediate limits to the extent one can bootstrap a model in this manner. I would argue that a bulk of scientific and mathematical reasoning is less statistically uncertain than the plot of a good fiction novel and that it may be the case that the societal value placed upon engineers is downstream of the rarity of individuals in the population with those skills rather than the statistical difficulty of many of those economically valuable tasks. While mathematical olympiad solutions or programming solutions may constitute a smaller portion of internet data than literary fiction, the data bottleneck they present may be more tractable from a predictive standpoint.